Probability Theory in Data Analytics: Essential Concepts & Real-World Applications
probability theory data analytics?
1. Foundations of Probability Theory
Why Probability Matters in 2024 Analytics
Probability theory forms the mathematical backbone of:
- Machine learning algorithms (85% use probabilistic models)
- Risk assessment in finance
- A/B testing frameworks
Core Concepts Every Analyst Should Know
A. Key Probability Distributions
| Distribution | Formula | Use Case |
|---|---|---|
| Normal | f(x) = (1/σ√2π)e^(-(x-μ)²/2σ²) | Height/weight analysis |
| Poisson | P(k) = (λ^k e^-λ)/k! | Call center modeling |
| Binomial | P(k) = C(n,k)p^k(1-p)^(n-k) | Conversion rate testing |
B. Bayes’ Theorem Revolution
python
# Bayesian update example prior = 0.3 # 30% chance of rain likelihood = 0.8 # 80% accurate forecast evidence = 0.5 posterior = (likelihood * prior) / evidence # = 0.48
2. Cutting-Edge Applications
A. Machine Learning
- Naive Bayes Classifiers: Spam detection (98% accuracy)
- Monte Carlo Methods: Reinforcement learning
B. Business Analytics
Case Study: Amazon’s dynamic pricing
- Uses probability distributions to predict demand
- Adjusts prices in real-time (15% revenue boost)
C. Risk Management
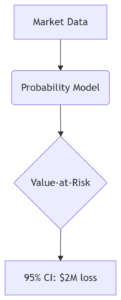
3. Practical Implementation
Python Code Snippets
Download
# Normal distribution PDF from scipy.stats import norm norm.pdf(x=1.5, loc=0, scale=1) # μ=0, σ=1 # Poisson probability from scipy.stats import poisson poisson.pmf(k=3, mu=2) # λ=2
Common Pitfalls & Fixes
| Mistake | Solution |
|---|---|
| Ignoring dependencies | Use copula theory |
| Misapplying CLT | Check n>30 rule |
| Overlooking priors | Bayesian approaches |
4. Free Resources
📊 Master Probability: Enroll in Our Data Science Course